Chart #1
Based on today's March unemployment claims report, some 22 million people (almost all from the private sector) have lost their jobs and are now subsisting on unemployment insurance (see Chart #1). This virus has returned US employment numbers to levels last seen at the depths of the Great Recession in late 2009. 11 years of progress have gone down the drain in a matter of weeks.
Chart #2
Although residential construction has been deemed to be "essential" (and its workforce thus allowed to continue working), home builders (red line in Chart #2) have suddenly lost almost all confidence in the future of their business. Housing starts have collapsed, but they will most likely fall further in the months to come. Such declines are sure-fire indicators of recessionary conditions. Think of the ripple effects of this on any number of industries dependent on housing.
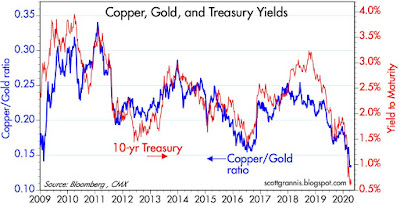
Chart #3
As Chart #3 shows, the ratio of copper to gold prices (blue line) has never before been so low. Traditionally, this ratio is strongly suggestive of the underlying growth dynamics of the US economy (a rising ratio being symptomatic of improving conditions, and vice versa). Moreover, 10-yr Treasury yields (red line) are now at all-time lows, which is also symptomatic of extremely weak economic growth potential. The only ray of hope I see here is that yields tend to move more at their extremes than does the copper/gold ratio, which in turn suggests that we may be at or close to the point of maximum weakness.
Chart #4
As Chart #4 shows, the shutdown of the US economy has had a profound impact on Americans' mobility. Gasoline demand has, almost overnight, fallen by roughly 50%. The only silver lining to this very dark cloud that I can see is the complete absence of traffic on Los Angeles-area freeways—and the utter disappearance of what little smog we had. This also illustrates how the law of unforeseen consequences works; force people to stay home, which forces many businesses to shut down, which sharply reduces commuter traffic, which slashes gasoline consumption, which leaves business that depend on mobile customers in the lurch (automobile dealers, gas stations, restaurants, malls, etc.) Overnight the economy has been subject to conditions that could never have been foreseen even in the worst of worst-case scenarios, and which impact almost every aspect of modern life. It's nothing short of a disaster. Thanks, politicians, for giving us a man-made disaster which surely eclipses the worst of earthquakes, tornadoes, and earthquakes. (Reminder: The shutdown of the US economy will prove to be the most expensive self-inflicted injury in the history of mankind. ™)
Chart #5
Chart #5 shows the average nationwide price of a gallon of regular gas at the pump. That it hasn't fallen further is likely a testament to the degree to which taxes now constitute a major portion of the cost to the consumer. I've seen reports that in some areas wholesale gasoline prices are near zero, and that's likely due to the fact that storage capacity has declined to absolute minimum levels.
Chart #6
Chart #6 illustrates the ratio of gold to crude oil prices. Never before has oil been so cheap relative to gold. That's the result of extremely low oil prices (~$20/barrel) and historically high gold prices (~$1700/oz.) Either gold is too expensive or oil is too cheap or some combination of the two. Such a sudden and radical change in relative prices is unlikely to persist for long. Will politicians please put on their pants and declare the shutdown over ...
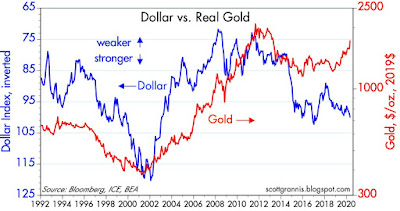
Chart #7
Chart #8
Chart #7 compares the value of the dollar (vis a vis a trade-weighted basket of other major currencies, and inverted), to the price of gold. Traditionally, periods of dollar weakness have coincided with periods of gold strength. But for the past two years or so we have seen the dollar and gold both strengthen. This is almost unprecedented, especially since, as Chart #8 shows, non-energy commodity prices have traditionally weakened as the dollar has strengthened and vice versa. Gold is the outlier these days. That could mean that the world is exceptionally risk-averse, or it could mean that the world fears that massive easing by the world's central banks will usher in a new era of rising inflation. Or both. I'll vote for the latter, but without maximum conviction.











45 comments:
Chart #1. Those are our fellow citizens tossed off the job by federal and state ukase. And the outlook is to add 5 million more unemployed for every week of lockdowns.
The lockdowns may or may not save an unknown number of lives, although that unknown number seems to be rapidly shrinking.
I am baffled by America's prominent macroeconomists. The government implements a depression, and they go mute. Perhaps there is no power greater than that of conventional thinking.
All hail Scott Grannis.
US Hospitals Receive As Much As $471,000 For Every COVID-19 Case They Report:
https://www.beckershospitalreview.com/finance/state-by-state-breakdown-of-federal-aid-per-covid-19-case.html
I have to rub my eyes when I see this: The S&P 500 is down 13% YTD, and the futures for Friday are up 3%.
Sheesh, that is a garden-variety correction.
I expected a 50% bear market, akin to 2009-9, or 2001-2, or 1973-4.
The market is saying officials will back down and end lockdowns.
I am delighted to be wrong, if I am. It still looks ugly out there to me.
Regina said:
>US Hospitals Receive As Much As $471,000 For Every COVID-19 Case They Report
That's a misleading, sensationalist statement.
MISLEADING #1: The article explicitly says that the $30 billion got initially distributed based on the historical share of Medicare revenue, "not based on COVID-19 burden"
MISLEADING #2: Within that context, the article explicitly says the money is how much each state is receiving per COVID-19 case, not how much hospitals are receiving per COVID-19 case.
SENSATIONALIST: By the same data, some states also receive as little as $12,000 for every COVID-19 case they report (that would be New York).
The mean average amount distributed is $171,431 per case, and the median is $166,000 per case. The difference in mean and median indicates it's a right-skewed distribution. And indeed, if you were to plot a histogram (which I did) you can clearly see the skew and that the $471,000 is a bit of an outlier.
Another way to get a sense of this is to compare the spreads of the five lowest payouts with the five highest.
The five lowest are: $12,000, $18,000, $23,000, $26,000, and $38,000. The spread is $26,000.
The five highest are: $315,000, $339,000, $379,000, $380,000, and $471,000. The spread is $156,000.
Again, you were misleading and sensationalist. It doesn't speak well of your opinion of the blog readers that you thought you could get away with it.
Bond markets staging a strong recovery. I'm having an excellent year. The stock and bond markets are not nearly as dour as this blog has become-and I never thought I would say that here!
Scott, are you taking downers? The markets are SCREAMING that things are not as bad as they appear. SURE, they could be wrong but I'd bet (well, I AM betting) with the bond markets than against them every time.
NOTE: the bond markets are NOT treasuries which are notoriously difficult/impossible to trade profitably. Look at HY credit, munies, bank loans, corporates, mortgage related-especially "sub-prime", preferreds. Almost anything that yields something is smoking right now.
And why not? The 10 year note is yielding .6%! That's the competition. So IF the world isn't falling off the cliff, other securities with much higher yields look attractive and that is the calculus.
CAVEAT EMPTOR. I am a trader and my opinion can turn on the dime and I could be 100% cash anytime. Barring another wave down, I don't see that happening soon-but it could.
S&P now off about 10% YTD. There's a reason for that. Too much gloom. Too many calling this a "bear market rally". I wrote a few days ago that there were positives to be observed during this calamity and one that has gone unnoticed is the resilience of the American people. Without question, the best of us comes out during extreme distress and this is no exception. Not to mention, energy prices are obviously WAY lower. Pollution is WAY down. Family unity is WAY up. I'm NOT going to predict a V economic recovery but I AM going to predict one that comes back faster than predicted.
Scott is voice in the wilderness.
The Emperor has no clothes
Nothing about this response respects Science.
The good news is accounts are pretty much back to even, YTD.
This was insanity.
None of this was warranted.
Stanford antibody test is already showing that this virus was 1/10th as deadly as flu.
It may be less.
Now, we are drowning in debt.
Scott, why don't you believe that the US hospital system would've collapsed had we not instituted a national/state-wide lock-down/quarantine? I'd be happy to hear from anyone else on this site/forum as well. Thank you.
Recently published in a number of Canadian local papers -- certainly looks coordinated!!!
Sir,
Not to appear xenophobic, but the US president’s desire to re-open the Canada/USA border fills me with anxiety. Canada has been a serious, united and largely acquiescent of most governments’ decisions vis-a-vis covid-19, we may disagree with the speed of re-opening the economy, but we all seem to agree that the governments took the right decisions and in general we have abided by the new and sometimes difficult rules that were put in place.
The US response has been, something else, and now it appears that the Federal government’s leader, President Donald Trump, is keen to foment rebellion in certain states – it may all come down to nothing, but it seems too well-coordinated – its smells like big money pushing “idiots gun-fodder ahead”. It also appears that China, Korea and Singapore’s new cases of Covid19 were largely caused by people traveling back to their country or visiting family.
I can see certain border adjacent Americans taking the opportunity to find shelter in Canada if they feel that the US system is putting them at risk. At the very least Canada should deploy its arm forces at the border to verify that all those crossing have available shelter when they “guarantee” they will remain isolated for 14 days. Americans are gun lovers, and their right-wing militias are just itching to “do something”. Their commander in chief seems to be giving them “carte blanche” to act stupidly, I think that the Prime Minister and his cabinet are right to want to wait another 30 days before opening the border to unlimited traffic, but more to the point Canada should have the resources in place to guard our frontiers.
It is a terrible thing to say, but America has behaved like an entitled teenager. Maybe its time for Canada to take care of its own!
Signed: A concerned citizen
This may make you think of what Canadians think of the US situation right now. We are hearing very bad things about the mid-West where medical facilities are poor and where few shelters in place rules have been enacted. The fear is that the world's longest "ungarded" border may
Steve said:
>Trump is an absolute embarrassment and an abysmal leader.
As H.L. Mencken allegedly said:
“As democracy is perfected, the office of the President represents, more and more closely, the inner soul of the people. On some great and glorious day, the plain folks of the land will reach their heart’s desire at last, and the White House will be occupied by a downright fool and a complete narcissistic moron.” -The Baltimore Evening Sun, 26 July 1920
It's time to reopen
Rick, as a SEAL officer you know better than anyone what a good leader looks like. The book "Extreme Ownership" written by two SEALs really delineates the qualities it takes to lead people effectively and our POTUS fails miserably at every turn.
Politics and policy are meaningless without the prerequisite qualities that define a good leader, the first and foremost of which is HUMILITY, something Trump doesn't even comprehend.
Steve,
Former SEAL officer.
That aside, I do know what a good leader looks like. I am honored to have served with more than my fair share of great leaders, Admiral Bill McRaven being one of them.
In my view, you could not pick a more pathetic example of a failed leader than Donald Trump. It's not just the humility that's lacking, it's the absolute refusal to accept any responsibility for how badly this whole thing has gone down.
I have said several times that the coronavirus is a good proxy for a biological warfare attack. Can you possibly imagine the President of the United States saying that individual Governors are responsible for protecting their states from a foreign biological warfare attack? It beggars the imagination...
We may be reaching a grim milestone.
According to the Centers for Disease Control, the mean average estimated number of deaths during flu seasons since 2010 that are due to influenza is 37,462. This includes nine flu seasons, and in particular it includes 2017 - 2018 when the number of deaths was inordinately high.
According the the Worldometer, the estimated number of deaths in the U.S. due to coronavirus -- now, at 12:24 pm EST on 18 April 2020 -- is 37,889
So, if these numbers be accurate, it is no longer a case of whether the coronavirus is as lethal as the flu. If these numbers be accurate, it is at least as lethal as the average estimates for a flu season.
Now the question is: how much worse is it going to get?
Will it top the average upper 95% CI for all the flu seasons, which I think was 54,300 deaths?
Will it top the highest upper 95% CI for the worst flu season – 2017–2018 – which I think was 95,000?
But who cares, right? Let's open the beaches in Florida!
Once a SEAL officer, ALWAYS a SEAL officer...
Scott your blog is on the top of my list and I also enjoy the comments with the likes of Benjamin Cole... But this March Madness has attracted a new crowd whose routes are disconnected from macro economics and lean towards conspiracy theories. I hope as the world normalizes the comment section returns to more productive discussion and Scott Grannis supportive. 32 years in the markets and you are the most sensible Economist. Thanks for all.
Rick, Steve -
Maybe I missed it - have you've opined with what criteria, how, and when the lockdown may unwind? Steve shared this link that touches on it:
https://www.nytimes.com/2020/04/06/opinion/coronavirus-end-social-distancing.html
And is there any space in your opinions to acknowledge the IHME projections have been way off the mark? Not just because of effective social distancing. But also because the projections were based on faulty assumptions and statistics, and assuming the rest of the country would look something like NYC and Italy - when the contributing factors of date of first exposures, avg age and health, population density, exposure to international travel, etc are all very different. There is a huge rabbit hole there that isn't possible to debate - but it seems reasonable that it doesn't make someone an idiot if they now question the decisions based on those faulty models. Yes, that's hindsight. It's also fair to say that those making decisions did the best they could with the information they had. Still - alternative history doesn't necessarily have to be completely unrestricted social interaction. There might have been other middle ground that would not have been worse. Do we repeat the path of making social distancing policies on the direst of possibilities?
I'm genuinely confused regarding how the strict lockdown defenders see the lockdown unwinding short of a near miracle treatment or vaccine. Not just in this blog but in the many podcasts and editorials I see. And without understanding how and when the lockdown may end, how can one possibly have any measure of optimism.
Mitigation saved exactly zero lives. The bell curve was "flattened" as well as lengthened however total number of infected is exactly the same in "un-flattened" bell curve. Yes, it may have bought some time to develop some therapies which may have saved lives, but the trade off is 22 million unemployed Americans and without a doubt an increase of drug and alcohol abuse, spousal,child and elder abuse as well as malnutrition, depression and suicide. Does it feel better to mitigate? To coastal elites evidently. Is it effective? Evidently not.
Quoting H L Mencken an anti-Semitic,racist bigot does nothing to prove your case. Surely you can find someone else to quote to bolster your case
Welschman said:
>Quoting H L Mencken an anti-Semitic, racist bigot...
Yeah, well, we call that an ad hominem attack.
>Yes, it may have bought some time to develop some therapies which may have saved lives...
Duh...
>..but the trade off is...without a doubt an increase of drug and alcohol abuse, spousal, child and elder abuse as well as malnutrition, depression and suicide.
Let's see...saved lives vs temporary decrease in quality of life. Hmmm...that's a tough one.
>Is it effective?
>Yes, it may have bought some time to develop some therapies which may have saved lives... You answered your own question.
A decrease in quality of life?
Asshat..yeah ad hominem
Bluntly, I find it almost beyond reason that in a 21st century society that we would allow mass deaths given the alternative to quarantine and without question reduce that number immeasurably. By "immeasurably" I mean we'll never know how many lives have been saved but it is unquestionably-except by those with their heads in the sand, factors more than without quarantine.
Furthermore, it's a MOOT point! The question now isn't whether quarantine was correct or not but rather, where do we go from here? Living in FL I am kinds embarrassed that our dumbass governor is reopening beaches. Pretty much guaranteeing reinfection in a state that has been somewhat spared.
As re reopening short of a vaccine, I hate to quote A Cuomo but he makes a hell of a lot more sense than Trump these days and he said "it's not a switch but rather a dial" or words to that effect. No easy answers and I suspect we'll experiment our way back to semi-normal until a vaccine shows up.
Welschman said:
>A decrease in quality of life?
Yeah, you know, if I had to choose between dying -- for me or a loved one -- or any of the quality of life issues you mentioned, I'm quite certain I'd choose the latter.
I mean, I know people who have died, and I know people who suffer from drug abuse, alcohol abuse, etc. Believe me, all those things you mentioned are better than dying because there is hope. There is no hope for a dead person.
@Welschman,
You know, on reflection, I think you're looking at this the wrong way.
Think of the lockdown and all the drug and alcohol abuse, spousal, child and elder abuse as well as malnutrition, depression and suicide that you mentioned as weeding out the weak and developing herd immunity -- have you heard that term before? -- for the climate change upheavals that are coming.
Attitude, pal, it's all a question of attitude.
Some of us have put our lives on the line for the quality of life issue more than once. Please don't question my attitude
>Some of us have put our lives on the line for the quality of life issue more than once.
Oh...I do beg your pardon. But do you think you are the only one whose life has been on the line more than once for quality of life issues?
Not at all
randy said:
>I'm genuinely confused regarding how the strict lockdown defenders see the lockdown unwinding short of a near miracle treatment or vaccine.
I'm not sure what you mean by "strict lockdown defender."
My own view is to ask a question that I try to ask in any important issue: "What is the cost or potential cost of being mistaken, and which of those costs I am more willing to bear?" That's not always the choice I make, but it's always a question I try to ask.
In the case of the coronavirus, I am more willing to bear the cost of over reacting than I am the potential cost of under reacting. And when I say that, I mean the costs or potential costs to society.
That said, one thing to do in situations like this is try to not get stuck in a false dilemma. Just because something gets initially framed as an "either-or" choice doesn't mean that's the only way to look at it.
Within that context, here is a suggestion from Pakistan, of all places, that looks relatively reasonable to me:
Smart Lockdowns
If you're really interested in developing an informed opinion about how the epidemiologists performed during the coronovirus thing...what some of the problems were...how they might be fixed...here you go...
Libertarian economist Tyler Cowan -- of George Mason University and the Mercatus Center -- posted some thoughts and some questions about epidemiologists: their salaries, their GRE scores, their political leanings, etc.
Here is his original blog post:
What does this economist think of epidemiology?
Here is the first response he got:
From my email: A note about epidemiology
And here are a few more:
More on economists and epidemiologists
Here is his most recent post on the topic...
Ahem
Enjoy!
Interesting reading there Rick. Here's an interesting thought; perhaps the reason the stock market is only down 10% YTD is because, like all "predictive analysis" the markets sees through inherent flaws of epidemiology models. Think about any predictive analysis. Based on data, they are still no better than a coin flip and usually worse. We only have to think about economics to come up with an example (this blog a noted and rare exception to the rule-usually). Another example would be stock market timing-a fools game if there ever was one. That's why I snicker when economists of all people push back against epidemiology models. Talk about the pot called the kettle black! The truth is predicting events is HARD. We listen to the "experts" because what other choice is there? It's easy now to say "We should never have quarantined" but we do not KNOW what would have happened had we not. That is unknowable. Best now to figure out the best way forward based on what we have learned and stop the bitching and moaning.
From the Ahem blogpost. "But I ask you, where are the numerous cases of leading epidemiologists screaming bloody murder to the press, or on their blogs, or in any other manner, that the most commonly used model for this all-important policy analysis is deeply wrong and in some regards close to a fraud?"
The first comment I saw: "They were busy attending a conference on modeling climate change."
Yes indeed.
I work in software engineering. I have a particular engineer that, with any given initiative, will write a 30 page white paper on the proper way to engineer, anticipating all the possible edge cases and outcomes, without regard to likelihood or cost benefit. The real world outcome is that he gets very little done, and when he does it's too often a mess of bloated complexity that doesn't perform well. Ironically, I recognize he's still valuable because he DOES sometimes have something very worthy to add. The trick for me is to decide what to keep and what to gently ignore.
We can anticipate the same thing happening with relaxing the lockdown. Given the defense of strict lockdowns (yes, there's that phrase again), we've dialed in that the benchmark of maximum caution. The Smart Lockdown link, and the NYT/WHO link, offer a glimpse of the theoretical highly managed relaxing of lockdown. This reminds me of my general problem with the left (E. Warren I've got a plan)... that they lack humility and historical perspective for how difficult and feckless it is to well manage complex social problems. Sure (sometimes) we have to try - but that's another story
Bottom line - without a vaccine or treatment, relaxing the lockdown will result in increased infections/deaths and risk of health system overload. All the smart policies in the world are not going to change that - or even mitigate it with any certainty. It's good to see lockdown defenders see some paths to relaxing. I can only hope policy makers accept the reality that risks can't be 100% managed, and get on with it.
>...perhaps the reason the stock market is only down 10% YTD is because, like all "predictive analysis" the markets sees through inherent flaws of epidemiology models.
I have a slightly different view. I think the stock market is on a sugar high from the Federal Reserve cash infusion, and because government bond yields are so low. I am doubtful this is sustainable. Maybe I'm wrong, but I am definitely doubtful.
Warren Buffett and his business partner, Charlie Munger, are big on what they call your "circle of competence," and only investing inside your circle of competence. Buffett says, "It doesn't have to be large, but it's vital that you know were the boundaries are."
I've been thinking about this lately. My own circle of competence is pretty small. Tiny, actually...a very niche industry (if you could even call it that). But I know what it is, and I make enough to satisfy my needs on it. I just dart in and out from time to time; make my yearly goal early, and get out.
I've probably watched a 30% rise go by over the past month because I've stayed out. I've asked myself, "Why?" And what I've come to realize is that my circle of competence is not just knowing a lot about about a niche service, it's also knowing something about market conditions. I have a sufficient enough understanding of normal market conditions to function well in them, but my circle of competence does not include understanding a stock market that is only down 10% year to date while every economist on the planet earth is predicting near economic collapse. I don't get it.
But fortunately I made my yearly goal by the end of January, and I don't really have to get it.
>It's easy now to say "We should never have quarantined" but we do not KNOW what would have happened had we not. That is unknowable.
I could not agree more with you here. That said, we will know some things as time goes on. For example, if you look at the Nordic countries Norway, Sweden, and Finland, I believe Norway and Finland took decisive action early, while Sweden did not. Today, Norway and Finland have 30 and 17 deaths per million, respectively, while Sweden has 152. I don't know if that's a valid comparison, but in time we might be able to say something meaningful about which approach was better in the long run.
I'd be willing to bet that when all the data is in (12-18 months from now) the CV19 profile will look eerily similar to the seasonal flu
>"I'd be willing to bet that when all the data is in (12-18 months from now) the CV19 profile will look eerily similar to the seasonal flu"
Can you post a link to the data sources / studies that shows covid-19 is highly weather dependent. I haven't been able to find any.
The IMHE model was designed to forecast hospital usage. Not death. Their death projections (60k) are understated. Their model is generally symmetric, while the reality is not.
Look at the Google mobility data. Both Spain and Italy are significantly more lockdowned than the US. Logic would suggest their new daily infections should decline steeper than the US.
While their lockdowns initially retarded new daily infections they haven't continued to meaningfully decline. More or less flat for the last 2-3 weeks.
Broad brush best case for the US, is ridiculously assuming new daily infections drop down to 15k tomorrow. And plateauing there for 3 weeks (based on Italy / Spain). Who knows what happens after that.
Approx 6.5% of confirmed are dying (based on confirmed cases 7 days earlier). So that's 975 dying daily for the next 3 weeks.
By early/mid May the US toll will be over 60k and counting.
A bad flu season of 60k deaths covers 6 months. Tell me again how covid-19 is like a bad flu, when the same number of deaths occurs in less than 2 months only after massive efforts have been undertaken to retard death....and we are still no where near the end of it.
David MacInnes: You may be right and we may see more than 60,000 COVID-19 related deaths in the US (mostly elderly with co-morbidities).
Still, with the virus becoming endemic globally (even in cats and dogs, evidently) you meet a problem.
I will paraphrase Joe Louis: "You can run, but you can't hide." Viruses do not lose patience.
We can stay in our hidey-holes for another 18 months, and if we are lucky, a vaccine will arrive. Suppose it does not?
And no one is certain we can repair the economy. Have you plans for quickly employing 50 million Americans? Clue us in. And 50 million may be a low estimate.
Yes, in dealing with COVID-19, all the options are bad. But what is the least-bad option?
First, you need excellent testing, which the US does not have.
Second, you need excellent contact tracing, which the US does not have.
Thirdly, you need a sufficiently low reproduction number, which the US does not have.
Fourthly, you need current cases at a manageable level, which the US does not have.
Once you do, the least bad option is some balance between staying at home and going to work.
Those that can work from home do so. Those that have social distance within their jobs go to work. Extend the work day, and break it into shifts with staggered starts to reduce contact within transport hubs. Consider making employees part time, rather than laying off - which loses knowledge base, and incurs significant recruitment costs down the line. There is a ton of ways to change the way we work to manage transmission AND the economy.
Humans are creative and adaptable, they will figure out a way to survive which doesn't involve sacrificing their parents.
>"And no one is certain we can repair the economy" - What is your timeframe? How do you suppose it will look in 5 years?
>"Have you plans for quickly employing 50m Americans?" - That would seem to imply going quickly back to a situation prior to Covid-19. But Covid-19 did happen. I can't suggest a method to bend reality. No.
I'd suggest the large majority of jobs have been lost temporarily, and as the economy slowly opens up, so will those same jobs. Was it painful? Yes (but it shouldn't have been for the large majority, ffs, you don't have enough savings to get you through a few months with no income - perhaps you need to look at your lifestyle and spending habits). Will it continue to be painful for those that permanently lost jobs? Yes. Would those people trade that pain to improve the odds to keep their parents? I don't know.
Are the 12-18 months up yet. Patience my friend
https://www.livescience.com/warmer-weather-slow-coronavirus-spread.html
Welschman...From your linked article
"Still, "we can't count on" the warmer and humid months to slow the spread of the virus"
"It's unreasonable, I think, at this point to expect that the virus will quote-on-quote disappear during our summer months,"
"Therefore its implication will be limited at least for northern European countries and northern U.S., which do not experience such warm temperatures until July, and that too for a very short time window,"
...not overly convincing that the warmer seasons will have a material effect....
David, yes there are a number of hedges in that article I agree but I was attempting to address your request for a link to weather dependent info re: COVID. Too soon to have any meaningful data (weather dependent or otherwise, IMO) which is why I originally mentioned using data harvested during the next 12-18 months.
Someone wrote:
"First, you need excellent testing, which the US does not have.
Second, you need excellent contact tracing, which the US does not have.
Thirdly, you need a sufficiently low reproduction number, which the US does not have.
Fourthly, you need current cases at a manageable level, which the US does not have.:
We do NOT need the first 2.
#3: You have no idea what that number is, but new evidence comes in every day that shows the Ro is less than we thought.
#4 cases are at completely manageable numbers, and always have been. Way less than seasonal flu.
If we weren't told this virus existed, nobody would even notice it in the data.
Given the early data on the antibodies tests, and early results on heat, light, humidity test I'll double down on the seasonal flu profile. Slightly more contagious, slightly deadlier but seasonal flu all the same.
Post a Comment